Begin
Determining WHIMC Exoplanet Sky Color
Our new scientist consultants from the University of Maine have been hard at work helping us to make the most accurate simulations possible for the Minecraft worlds of Project WHIMC. We recently asked Bryce Roix to share some of his work process in determining how we should color the skies of our exoplanets with Datapacks.
Convolution of the Blackbody Equation and the Rayleigh Scattering Equation for Molecules: Attempt #1
The purpose of this work is to determine the sky color of exoplanets. By using Planck’s Law, the blackbody equation, in conjunction with the Rayleigh Scattering Equation for molecules the intensity of scattered light can be calculated. This work will be done using arbitrary variables, specifically variables that are characteristic to the solar system in question, allowing us to apply this work in other scenarios. Units in this work are enclosed by square brackets [ ].
To begin, Planck’s Law in terms of wavelength states:

Constants in equation 1:
- 𝑘 = 1. 38065 * 10-23 [ J/K] Boltzmann constant
- ℎ = 6. 62607 * 10-34 [Js] Planck’s constant-
- 𝑐 = 2. 99792 * 108 [m/s]
Speed of light in a vacuumReader set variable: - 𝑇 = temperature of host star [K]
Stars are essentially perfect blackbodies, equation 1 describes the spectral radiation emitted from a star. An explanation of units in equation 1: 𝐵(λ, 𝑇) represents the power [W]2 or [J/s] per unit area [1/𝑚2]per unit solid angle, θand φ with units [1/𝑟𝑎𝑑2], per wavelength of light [1/𝑚].
The Rayleigh scattering equation for molecules utilized properties of the molecule as well as the incident light intensity. The equation for Rayleigh scattering is represented in equation 2.
Rayleigh Scattering of Light for Molecules states:
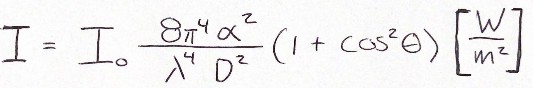
- Constants in equation 2:
- λ =wavelength of incoming light [m]
- α =polarizability of molecule [𝑚3]
- 𝐷 = distance from the observer to the location of scattering [m]2
- 𝐼 ◦ = Intensity of incident light [𝑊/𝑚2 ]Reader specified variable:
- θ = Angle of scattered light
A quick sketch of the light scattering process to help visualize the scattering angle θ and light interaction with molecules is drawn in figure 1.
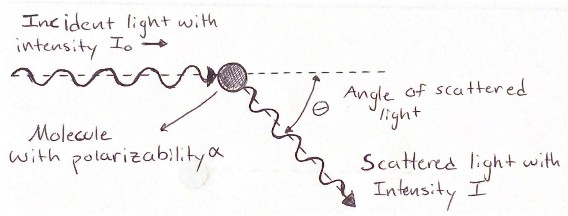
The thought process for this work begins with the relating the blackbody equation to the intensity of incoming light 𝐼 ◦in equation 1, which is dependent on the temperature of the blackbody. A quick unit comparison between 𝐵(λ, 𝑇) [𝑊/𝑟𝑎𝑑2𝑚3]and 𝐼 ◦ [𝑊/𝑚2]. Equation 1 represents radiation emitted from a region of area on the surface of a sphere, in this case the sun. The distance between the sun and the Earth is much greater in comparison to the radius of the Earth leading to the use of the small angle approximation for the angle of incident light. This approximation allows us to assume that the photon emitted from the sun are parallel to one another. A drawing of parallel light striking a differential surface area on the Earth’s atmosphere is represented by figure 2.
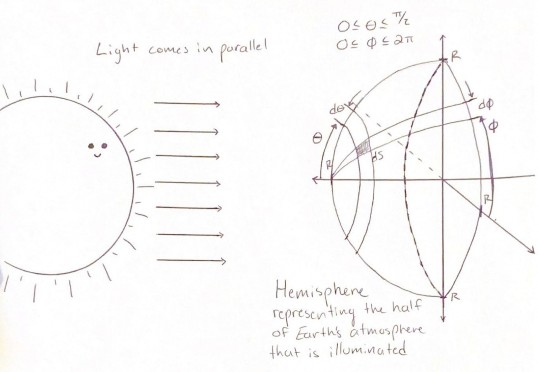
Assuming the earth atmosphere is spherical, the equation for blackbody radiation has been integrated over the differential surface area of a hemisphere dS. The solid angles that form a hemisphere for θand φ have the ranges: 0 ≤ θ ≤ π and 0 ≤ φ ≤ 2π. The differential surface area value for dS is shown in equation 3, where we define a new variable, R the radius of the atmosphere in question. dS has units of [𝑚2𝑟𝑎𝑑2] The equation for integration of Planck’s Law is as follows. Note the units of the final metric.
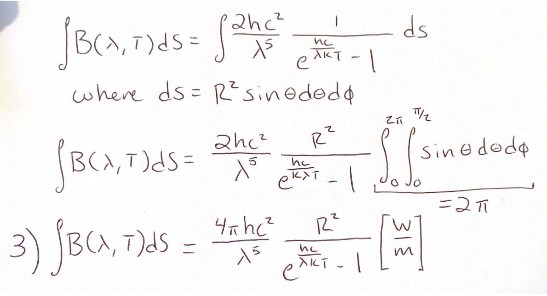
Upon completion of the integration the units of this equation are [W/m]. We are attempting to manipulate equation 1 into the variable 𝐼◦, with units [𝑊/𝑚 ], mentioned in equation 2 the Rayleigh scattering of molecules. To achieve the proper units, next we will differentiate equation 4 with respect to the wavelength of light λ [m], to get the appropriate units of intensity [𝑊/𝑚 ]. The derivative of equation 3 now, in theory, equates 𝐼 ◦ which is equation 4. WolframAlpha was used to perform this integration.
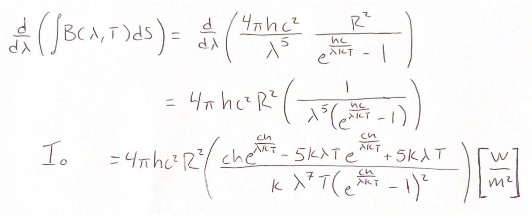
We can now take this differentiated equation for the variable 𝐼 ◦ and plug it into the equation for Rayleigh scattering. Doing so gives equation 5 with the proper units.

We now have an equation for Rayleigh scattering that is dependent on the temperature of the blackbody and the wavelength of the incoming light. Four variables in equation 5 are reader defined: 𝑇, θ, 𝑅, & 𝐷. We are assigning these values as follows: 𝑇 = 6000𝐾 and θ = 45°. θ is arbitrarily defined as 45°.
The values of R and D are dependent on the atmospheric composition of the selected planet. For Earth’s atmosphere, the layer in which the atmosphere absorbs the most electromagnetic radiation is the Ozone layer. Specifically a layer of 𝑂3 molecules that has a thickness of 6 * 10 𝑚. Located in Earth’s atmosphere, 𝑂3 absorbs and scatters radiation from the sun which is the primary reason for the blue color of the sky as viewed from Earth’s surface. The polarizability of 𝑂3 is α = 3. 079 * 10-26 𝑚 . Assuming that the Earth, as well as Earth’s atmosphere, are spherical we define R and D.
Atmospheric radius: 𝑅 = 𝑟𝑎𝑑𝑖𝑢𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑒𝑎𝑟𝑡ℎ + 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑡𝑜 𝑂𝑧𝑜𝑛𝑒 𝑜𝑢𝑡𝑒𝑟 𝑒𝑑𝑔𝑒
Observation distance: 𝐷 = 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑡𝑜 𝑜𝑧𝑜𝑛𝑒 𝑜𝑢𝑡𝑒𝑟 𝑒𝑑𝑔𝑒
The next figure is a sketch of the location of scattering. Rayleigh scattering occurs at various locations at a depth in the atmosphere. For simplicity, the intensity of scattered light will be calculated on the outer edge of the Ozone layer. The next figure 3 helps visualize these lengths.
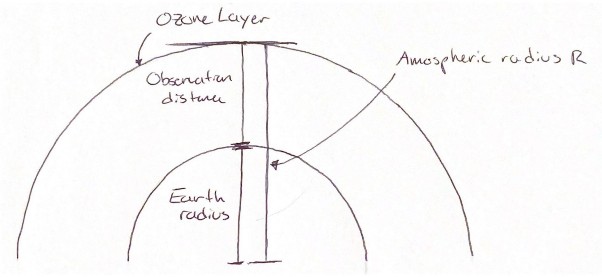
The observation distance is the length from the Earth’s surface to the outer edge of the
Ozone layer: 𝐷𝑜𝑧 = 16 * 103 𝑚
Atmospheric radius of ozone layer: 𝑅 = 16 * 103 + 6. 371 * 106 𝑚 = 6. 387 * 10 𝑚
Now we can plug in all defined variables into equation 2 to get the convolution for the intensity of scattered light with respect to the incident wavelength. Implementing the following constants 𝑘. ℎ. 𝑐, 𝑇, θ, α, 𝑅, & 𝐷. We get the following reduced metric from equation 2, represented in the following equation 5.
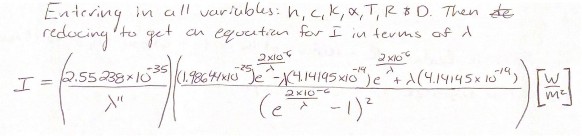
This equation is not inherently intuitive. The value of incident wavelength is unknown. The host star, our blackbody, emits all wavelengths of light. However there is a peak wavelength of light that is dependent on the temperature of the blackbody. This peak wavelength is defined using Wein’s displacement law. This law yields a maximum wavelength of light
emitted by the blackbody. Keeping the equation of scattered light intensity arbitrary in terms of incident wavelength, we can graph this function to get a visual representation of the scattered intensity in terms of incident wavelength. Graphing equation 5 yields the following images in figure 4. Graphing of equation 5 was done using Desmos graphing calculator.
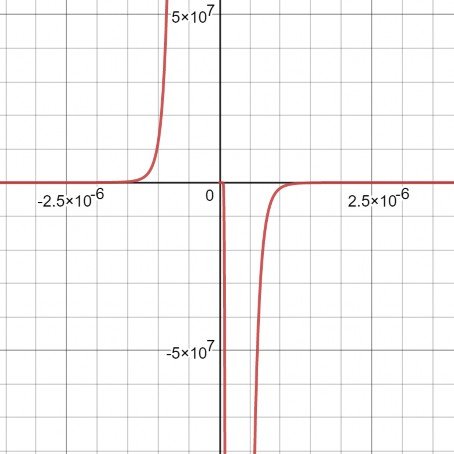
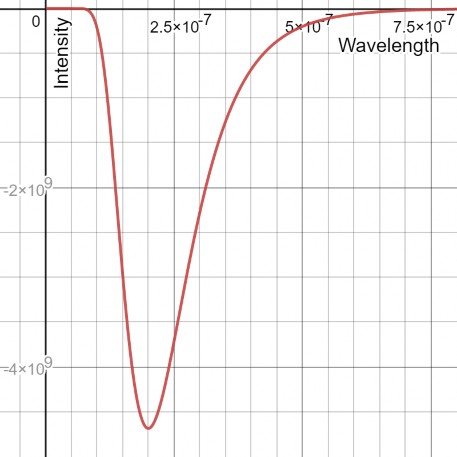
Figure 4 shows two images of the same graph. Image A shows the asymptotic left side of the graph in the negative wavelength axis. Image B shows the right side of the graphs along the positive wavelength axis. There is a minimum located in the trough of the graph at the point (2 * 10-7, − 4. 6873 * 109). The incident wavelength is λ = 2 * 10-7 [𝑚] using this value we can quickly calculate the incident intensity of a photon with the same wavelength using equation 6.
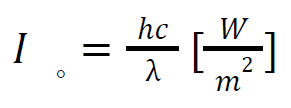
Performing this calculation the value of 𝐼◦ is:
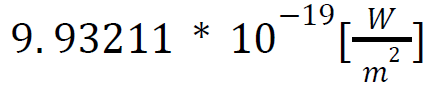
We can now take this incident light intensity value 𝐼 ◦ , as well as the incident wavelength value λ and plug both into equation 2. Where we expect to get the value of scattered light intensity at the peak wavelength, shown in figure 4B, with a value of:
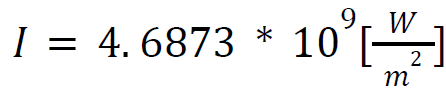
Noting here that value of intensity is taken as an absolute value knowing that all variables in equation 6 are positive. Now performing the calculation from equation 2 with the new 𝐼 ◦ and λ, keeping all other variables the same as previous calculations we get the following value of intensity for scattered light.

This calculation of scattered light intensity does not equal the intensity value shown in the figure 4B graph, where at wavelengthλ = 2 * 10-7 [𝑚] scattered light intensity is:
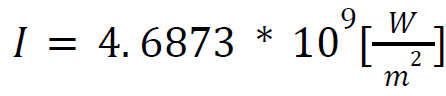
Although this work did not achieve the desired scattered light intensity, more attempts to relate Planck’s Law to the Rayleigh Scattering equation for Molecules. Each attempt will be documented and written similarly to the work done for this first attempt.

